Students who jumped at the question would be scratching their heads. Students who overthink at the question would probably still thinking about it today. Students who are weak would offer an excuse that the question didn’t come with sufficient information. But for students with good logical thinking, they could solve it in seconds.

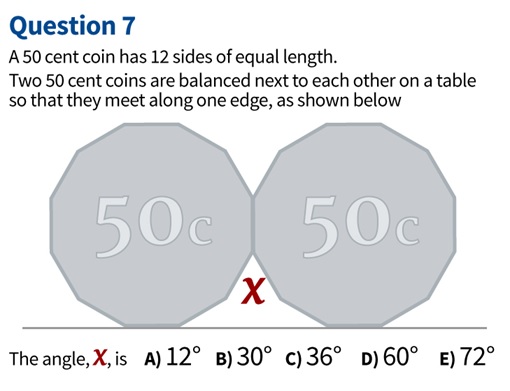
Behind the question that has left Australian Victorian High School (VCE) students stumped and venting their fury was a maths question prepared for the Year-12 VCE Further Maths examination. The multiple choice question asked students to look at two 50-cent coins with 12 sides each – which are known as “dodecagons” – and find the degree of the angle between them.

 

The question reads – “A 50 cent coin has 12 sides of equal length. Two 50 cent coins are balanced next to each other on a table so they meet along one edge.” Students were then asked to select from five options from 12, 30, 36, 60 to 72 degrees. VCE Further Maths students have been debating the tougher question in the subject’s exam on Friday.

Needless to say, many have taken to the social media to express their anger. Even rapper Curtis James Jackson III, better known as 50 Cent, didn’t survive the VCE students’ curse when one of them posted – “Fuck You 50 Cent. I never liked your music anyway.” Another wrote – “That exam wasn’t there to test us, it was to trick, no one could of prepared for that.”

 

Student Daphne said – “It was quite different to the ones we had been doing. I did find it challenging … under the stress of the exam. I found it a little ambiguous and confusing. I think I was over thinking it.” While one student complained “It was a shitty question”, another said “Still trying to figure out the angle.”

But teachers deny the question was too difficult because a logical thinking student would be able to solve it within seconds. Sunshine College teacher Graeme Newman said while the 50 cent question was challenging, nevertheless he believed the two parts of the exam, which were on Friday and Monday, were fair.

 

Ever since the frustrated students took it to the social media, condemning the question, it also invited retaliation from people who insulted the students, arguing that the question was actually too simple to even be in a Year 12 exam. “This seriously took me 10 seconds to solve. Stop your whinging kids!” Adam Astill wrote on Facebook.

So, what’s the solution for the 50-cent maths question?

• The sum of all the exterior angles in any shape will always be 360°.
• Therefore, the exterior angle of one of the sides can be worked out by: 360°/12 = 30°
• This number must then be multiplied by two, because the angle is where two exterior angles meet.
• Therefore the answer is found by (360°/12) x 2 = 60°

 

The answer can also be found by using formula based on the interior angles of a polygon.

• There are 12 angles inside the polygon.
• The interior angles of the coin are calculated using the rule 180n-360
• The total interior angle sum of the coin is 1800°
• When divided by the number of sides – 12 – you find each interior angle is 150°
• As the interior angle is 150°, the exterior angle is 30° as a straight line is 180°
• The exterior angle must be multiplied by two to find the answer: 60°

 

Other Articles That May Interest You …

• Budget 2016 – What Najib Razak Doesn’t Want You To Know
• Top Student Gets 7 “Zeroes” – Egyptian Most Absurd Corruption Case
• Can You Solve This Hong Kong Exam Question For 6-Year-Old, In 20-Seconds?
• Here’s How Your “Wave & Pay” Cards Could Be Swiped Secretly
• One More (Secret) Thing … Apple iOS 8 Allows Wireless Charging Using MicroWave
• Another Reason To Eat More Chocolate – It Can Reverse Memory Loss
• Maths Genius Sufiah enjoys Sex career, no Regrets

Tweet

November 3rd, 2015 by financetwitter

If you enjoyed this post, what shall you do next? Consider: